Estrategia de Control de Proceso: Aplicación de Promedio, Desviación Estándar, Tz, Cr, Cp y Cpk

El control estadístico de procesos es una herramienta esencial en la gestión de calidad moderna. Comprender y aplicar correctamente conceptos estadísticos como el promedio, la desviación estándar, Tz (Target Z), Cr (Capability Ratio), Cp (Índice de Capacidad del Proceso) y Cpk (Índice de Capacidad del Proceso Real) es fundamental para garantizar procesos eficientes y productos de alta calidad.

Este artículo ofrece una guía sobre cómo implementar una estrategia de control de proceso utilizando estas herramientas estadísticas. Abordaremos definiciones, fórmulas, interpretaciones geométricas y pasos prácticos para su aplicación, proporcionando un recurso integral para ingenieros de control de calidad.

Introducción al Control Estadístico de Procesos

El Control Estadístico de Procesos (SPC, por sus siglas en inglés) es una metodología que utiliza técnicas estadísticas para monitorear y controlar un proceso de producción. El objetivo principal es identificar y eliminar causas especiales de variación, asegurando que el proceso funcione de manera eficiente y consistente dentro de los límites de especificación.

Importancia del SPC

• Mejora Continua: Facilita la identificación de oportunidades para mejorar procesos y productos.
• Reducción de Costos: Al minimizar el desperdicio y el retrabajo, se reducen los costos operativos.
• Satisfacción del Cliente: Garantiza que los productos cumplen con las especificaciones y expectativas.
• Competitividad: Mejora la posición en el mercado al ofrecer productos de alta calidad de manera consistente.

Fundamentos Estadísticos

Antes de profundizar en las herramientas específicas, es esencial comprender los conceptos estadísticos básicos que subyacen al SPC.

Promedio (X)

El promedio es una medida de tendencia central que representa el valor típico de un conjunto de datos.

Fórmula:

Interpretación:

• Representa el punto central alrededor del cual los datos están distribuidos.
• Es sensible a valores atípicos (outliers), por lo que debe interpretarse con cautela en presencia de datos extremos.

Desviación Estándar (σ)

La desviación estándar mide la dispersión de los datos alrededor del promedio, indicando cuánto varían los valores individuales.

Fórmula para una muestra:

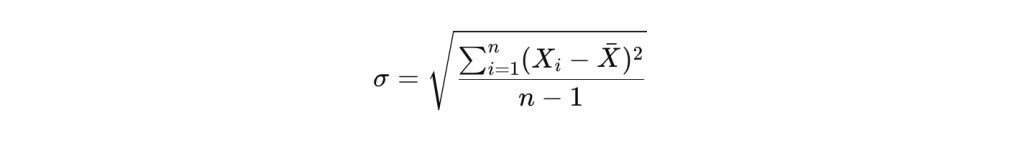
Interpretación:

• Una desviación estándar pequeña indica que los datos están agrupados cerca del promedio.
• Una desviación estándar grande sugiere que los datos están más dispersos.

Importancia en SPC:

• La desviación estándar es clave para calcular los índices de capacidad del proceso.
• Ayuda a identificar la variabilidad inherente del proceso.

Variables Clave en el Control de Procesos

1. Índice de Capacidad del Proceso (Cp)

Definición:

El Cp es una medida de la capacidad potencial de un proceso para producir resultados dentro de los límites de especificación, sin considerar la ubicación del promedio del proceso.

Fórmula:

• LSE: Límite Superior de Especificación.
• LIE: Límite Inferior de Especificación.
• σ: Desviación estándar del proceso.

Interpretación:

• Cp ≥ 1: El proceso tiene la capacidad potencial para cumplir con las especificaciones.
• Cp > 1.33: Se considera que el proceso es altamente capaz.
• Cp < 1: El proceso no es capaz de cumplir con las especificaciones de manera consistente.

Limitaciones:

• No considera la centralización: Un Cp alto no garantiza que el proceso esté centrado entre los límites de especificación.

Aplicación Práctica:

• Utilizado en las etapas iniciales para evaluar si el proceso tiene la variabilidad adecuada para cumplir con las especificaciones.

2. Índice de Capacidad del Proceso Real (Cpk)

Definición:

El Cpk mide la capacidad real del proceso, teniendo en cuenta tanto la variabilidad como la centralización respecto a los límites de especificación.

Fórmula:

Interpretación:

• Cpk ≥ 1.33: El proceso es capaz y está bien centrado.
• Cpk ≥ 1: El proceso es capaz pero puede requerir mejoras.
• Cpk < 1: El proceso no es capaz y necesita acciones correctivas.

Importancia:

• Considera la centralización: Un Cpk alto asegura que el proceso está produciendo dentro de las especificaciones con una baja tasa de defectos.

Relación con Cp:

• Si el proceso está perfectamente centrado, Cpk = Cp.
• Si el proceso está descentrado, Cpk < Cp.

3. Target Z (Tz)

Definición:

El Tz mide el corrimiento del proceso, es decir, la desviación del promedio del proceso respecto al valor objetivo, expresado en unidades de desviación estándar.

Fórmula:​

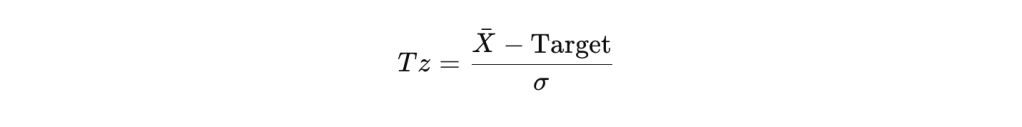
• Target: Valor objetivo o nominal para la variable.

Criterio de Éxito:

• Tz < 0.5: El corrimiento del proceso está bajo control.

Interpretación:

• Tz positivo: El promedio está por encima del objetivo.
• Tz negativo: El promedio está por debajo del objetivo.
• Tz cercano a cero: El proceso está centrado en el objetivo.

Interpretación Geométrica de Tz:

• Visualización:
  • Tz representa la distancia entre el promedio del proceso y el valor objetivo en términos de desviaciones estándar (σ).
• Desplazamiento Máximo Permitido:
  • Un Tz < 0.5 significa que el promedio del proceso está dentro de 0.5σ del valor objetivo.
• Gráfico:
  • La distribución normal del proceso está casi centrada en el valor objetivo, con una desviación mínima permitida.

Importancia Práctica:

• Minimiza Productos Fuera de Especificación:
  • Al mantener el corrimiento bajo control, se reduce la probabilidad de producir productos no conformes debido a un promedio descentrado.
• Asegura Calidad Consistente:
  • Un proceso centrado produce resultados más predecibles y uniformes.

4. Rango de Capacidad (Cr)

Definición:

El Cr es una medida de la relación entre la variabilidad del proceso y el rango de especificación, siendo el inverso del Cp.

Fórmula:​

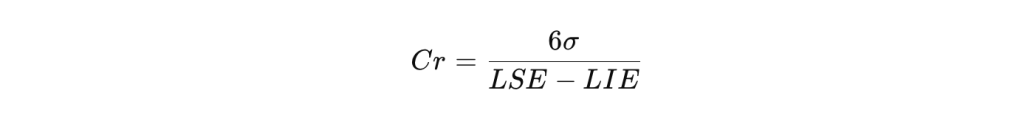
Criterio de Éxito:

• Cr < 0.75: La variabilidad del proceso está bajo control.

Interpretación:

• Cr < 1: La variabilidad del proceso es menor que el rango de especificación.
• Cr > 1: La variabilidad del proceso excede el rango de especificación.

Interpretación Geométrica de Cr:

• Visualización:
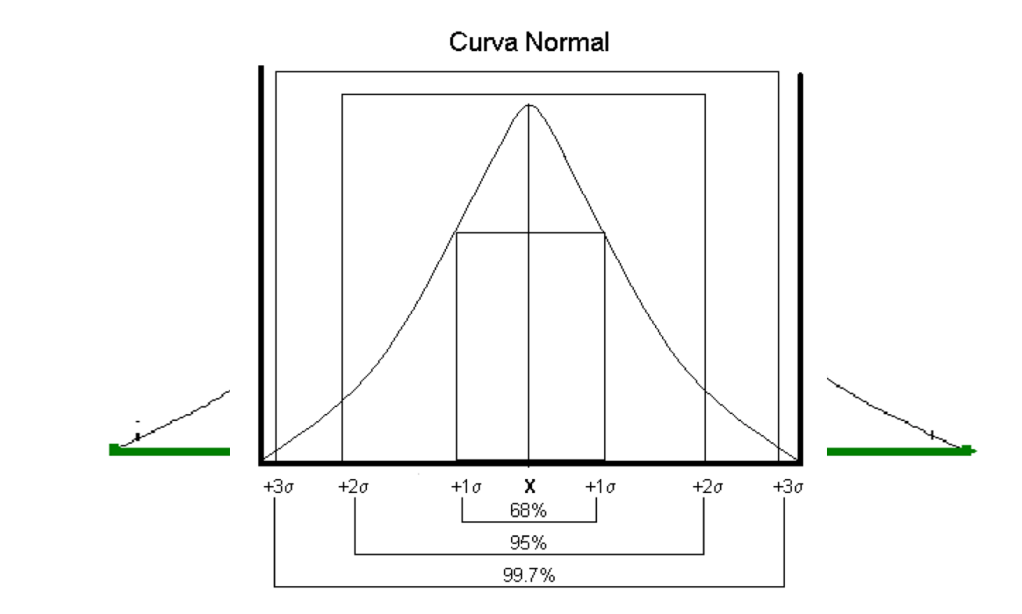
  • Cr indica cuánto de la variabilidad total del proceso (6σ) ocupa el rango de especificación.
• Zona de Seguridad:
  • Un Cr < 0.75 implica una zona de seguridad del 25% del rango de especificación no ocupada por la variabilidad del proceso.
• Distribución Equitativa:
  • Si el proceso está centrado, esta zona de seguridad se divide en 12.5% en cada extremo del rango de especificación.
• Gráfico:
  • La curva de la distribución normal es más estrecha que el rango de especificación, proporcionando márgenes de seguridad.

Importancia Práctica:

• Control de Variabilidad:
  • Reduce la probabilidad de producir productos fuera de especificación debido a variaciones inherentes en el proceso.
• Permite Tolerancia a Pequeñas Fluctuaciones:
  • El margen de seguridad absorbido por un Cr bajo permite acomodar variaciones sin comprometer la calidad.

Implementación de la Estrategia de Control de Proceso

A continuación, se presentan los pasos detallados para implementar una estrategia de control de proceso utilizando las variables clave.

Paso 1: Recolección de Datos

Muestra Mínima Requerida:

• 29 datos es el mínimo recomendado para asegurar una estimación confiable de la variabilidad y el promedio del proceso.

Consideraciones:

• Representatividad:
  • Los datos deben ser representativos del proceso bajo condiciones normales de operación.
• Frecuencia de Muestreo:
  • Determinar una frecuencia que capture la variabilidad del proceso sin sobrecargar el sistema de recolección de datos.

Justificación Estadística:

• Una muestra de al menos 29 datos proporciona suficiente información para estimar parámetros estadísticos con un nivel aceptable de precisión.

Paso 2: Cálculo del Promedio y Desviación Estándar

Cálculo del Promedio (Xˉ):

• Sumar todos los valores y dividir por el número de observaciones.

Cálculo de la Desviación Estándar (σ):

• Utilizar la fórmula de la desviación estándar muestral para reflejar la variabilidad del proceso.

Validación de Datos:

• Detección de Valores Atípicos:
  • Identificar y analizar valores que se desvíen significativamente del resto de los datos.
• Análisis de Normalidad:
  • Verificar si los datos siguen una distribución aproximadamente normal, requisito para la aplicación correcta de los índices de capacidad.

Paso 3: Determinación de los Límites de Especificación y Valor Objetivo

Límites de Especificación:

• LIE (Límite Inferior de Especificación): Valor mínimo aceptable.
• LSE (Límite Superior de Especificación): Valor máximo aceptable.

Valor Objetivo (Target):

• El valor ideal o nominal que se desea alcanzar en el proceso.

Consideraciones:

• Los límites y el objetivo deben estar claramente definidos y ser realistas en función de las capacidades del proceso y los requisitos del cliente.

Paso 4: Cálculo de Cp y Cr

Cálculo de Cp:

Interpretación de Cp:

• Cp > 1.33: Indica que el proceso tiene potencial para cumplir con las especificaciones con un margen de seguridad.

Cálculo de Cr:

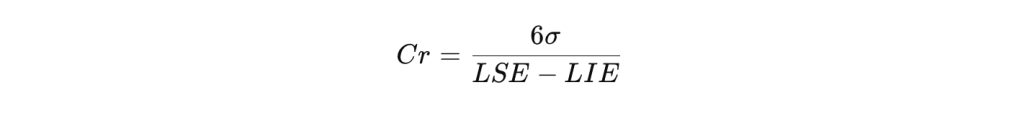
Interpretación de Cr:

• Cr < 0.75: La variabilidad está bajo control, proporcionando un margen de seguridad del 25% del rango de especificación.

Interpretación Geométrica de Cr:

• Visualizar cómo la distribución del proceso se ajusta dentro del rango de especificación con márgenes adecuados en ambos extremos.

Paso 5: Cálculo de Tz

Cálculo de Tz:

Análisis de Tz:

• Determinar si el corrimiento del proceso está bajo control (Tz < 0.5).

Interpretación Geométrica de Tz:

• Visualizar el desplazamiento del promedio del proceso respecto al valor objetivo en términos de desviaciones estándar.

Paso 6: Cálculo de Cpk

Cálculo de Cpk:

Análisis de Cpk:

• Determinar la capacidad real del proceso considerando la variabilidad y la centralización.

Interpretación de Cpk:

• Un Cpk ≥ 1.33 indica que el proceso es capaz y está centrado adecuadamente.

Paso 7: Análisis de Resultados

Interpretación Conjunta:

• Cp y Cr: Evaluación de la variabilidad del proceso.
• Tz: Evaluación del corrimiento del proceso.
• Cpk: Evaluación de la capacidad real del proceso.

Identificación de Áreas de Mejora:

• Si Cp es adecuado pero Cpk es bajo, el problema es de centralización (corrimiento).
• Si tanto Cp como Cpk son bajos, el problema es de variabilidad y centralización.

Toma de Decisiones:

• Proceso Capaz y Centrado: Continuar con el monitoreo estándar.
• Proceso Incapaz o Descentrado: Implementar acciones correctivas.

Paso 8: Implementación de Acciones Correctivas

Reducir la Variabilidad (Mejorar Cr y Cp):

• Mantenimiento Preventivo: Asegurar que el equipo funcione correctamente.
• Capacitación del Personal: Mejorar las habilidades y el conocimiento del operador.
• Control de Proveedores: Garantizar la calidad de las materias primas.
• Optimización de Parámetros: Ajustar condiciones de operación para reducir variaciones.

Centrar el Proceso (Mejorar Tz y Cpk):

• Ajuste de Máquinas: Calibrar equipos para alinear el promedio con el objetivo.
• Establecer Procedimientos Estandarizados: Reducir variaciones en la ejecución del proceso.
• Implementar Control Automático: Utilizar sistemas de control para mantener el proceso centrado.

Paso 9: Monitoreo Continuo

Gráficos de Control:

• Gráficos X̄-R: Monitorear el promedio y el rango de subgrupos de datos.
• Gráficos de Tendencia: Identificar patrones o tendencias a lo largo del tiempo.

Análisis Estadístico Regular:

• Revisión de Índices de Capacidad: Actualizar Cp, Cpk, Tz y Cr periódicamente.
• Auditorías Internas: Verificar el cumplimiento de procedimientos y estándares.

Feedback y Mejora Continua:

• Comunicación Efectiva: Compartir resultados y hallazgos con el equipo.
• Planificación de Acciones Futuras: Basar decisiones en datos y análisis estadísticos.

Ejemplo Ilustrativo

Contexto

• Industria: Fabricación de piezas mecánicas de precisión.
• Proceso: Mecanizado de ejes cilíndricos.
• Variable Crítica: Diámetro del eje.
• Límites de Especificación:
  • LIE: 19.95 mm.
  • LSE: 20.05 mm.
• Valor Objetivo (Target): 20.00 mm.

Recolección de Datos

• Muestra: 30 mediciones del diámetro tomadas en condiciones normales.
• Resultados Obtenidos:
  • Xˉ: 20.01 mm.
  • σ: 0.025 mm.

Cálculos

1. Cp:

Interpretación:

• Cp < 1: El proceso no es capaz de cumplir con las especificaciones.

2. Cr:

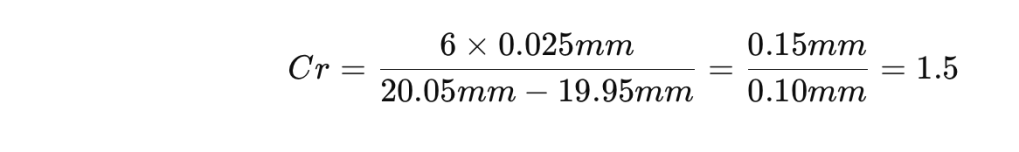
Interpretación Geométrica:

• Cr > 1: La variabilidad del proceso excede el rango de especificación.

3. Tz:

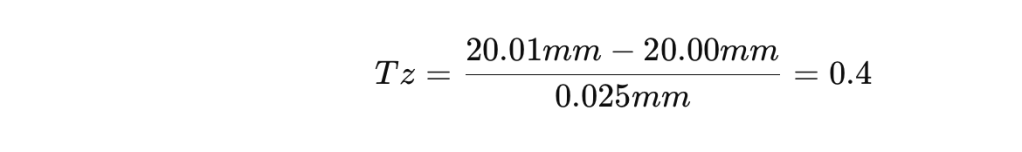
Interpretación:

• Tz < 0.5: El corrimiento está bajo control.

4. Cpk:

Interpretación:

• Cpk < 1: El proceso no es capaz.

Análisis de Resultados

• Variabilidad Excesiva:
  • Cp y Cr indican que la variabilidad del proceso es demasiado alta para el rango de especificación.
• Corrimiento Aceptable:
  • Tz muestra que el proceso está centrado cerca del valor objetivo.
• Capacidad Insuficiente:
  • Cpk confirma que el proceso no es capaz de cumplir consistentemente con las especificaciones.

Acciones Correctivas

Reducir la Variabilidad:

• Mantenimiento de Equipos:
  • Revisar y calibrar las máquinas de mecanizado.
• Optimización de Parámetros:
  • Ajustar velocidades y avances para mejorar la precisión.
• Capacitación del Personal:
  • Entrenar a los operarios en técnicas de control y ajuste fino.

Monitoreo Intensivo:

• Incrementar la Frecuencia de Muestreo:
  • Detectar y corregir variaciones más rápidamente.
• Implementar Gráficos de Control:
  • Monitorear en tiempo real el comportamiento del proceso.

Seguimiento

• Reevaluar después de las Acciones:
  • Recopilar una nueva muestra y recalcular los índices.
• Objetivo:
  • Alcanzar un Cp y Cpk ≥ 1.33, y un Cr < 0.75.

Otros Ejemplos Prácticos

Ejemplo 1: Con Resultados Satisfactorios

Contexto:

• Proceso: Fabricación de ejes metálicos.
• Variable: Diámetro del eje.
• LIE: 49.5 mm.
• LSE: 50.5 mm.
• Target: 50.0 mm.

Datos Recolectados:

• n: 30.
• Xˉ: 50.02 mm.
• σ: 0.15 mm.

Cálculos:

• Tz:

Interpretación: Tz < 0.5; corrimiento bajo control.

• Cr:

Interpretación: Cr = 0.9; ligeramente superior al criterio, pero aceptable.

• Cp:

Interpretación: Cp > 1; proceso potencialmente capaz.

• Cpk:

Interpretación: Cpk > 1; proceso capaz.

Interpretación Gráfica:

• Tz:
  • La curva de distribución está centrada cerca del valor objetivo, con el pico muy próximo a 50.0 mm.
• Cr:
  • La distribución es ligeramente más ancha, pero aún dentro de los límites de especificación, con márgenes aceptables.

Conclusión:

• Resultados Satisfactorios: El proceso es capaz y está centrado adecuadamente.

Ejemplo 2: Algunas Variables Cumplen y Otras No

Contexto:

• Proceso: Producción de tornillos.
• Variable: Longitud del tornillo.
• LIE: 19.0 mm.
• LSE: 21.0 mm.
• Target: 20.0 mm.

Datos Recolectados:

• n: 30.
• XˉXˉ: 20.3 mm.
• σσ: 0.4 mm.

Cálculos:

• Tz:

Interpretación: Tz > 0.5; corrimiento excesivo.

• Cr

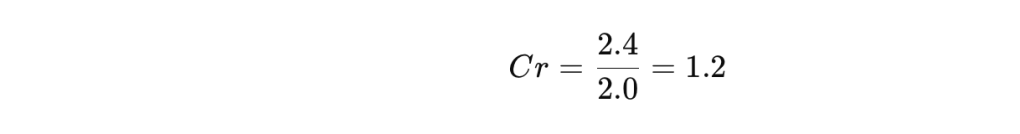
Interpretación: Cr > 0.75; alta variabilidad.

• Cp

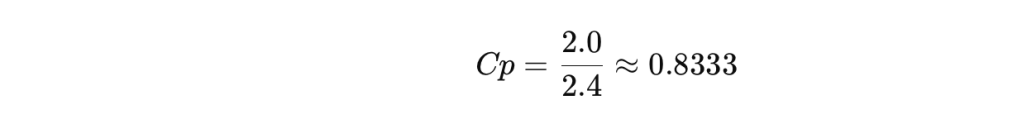
Interpretación: Cp < 1; proceso no es capaz.

• Cpk:

Interpretación: Cpk < 1; proceso no es capaz.

Interpretación Gráfica:

• Tz:
  • La curva de distribución está desplazada hacia la derecha, alejándose del valor objetivo de 20.0 mm.
• Cr:
  • La distribución es ancha, sobrepasando los límites de especificación, lo que indica alta variabilidad.

Conclusión:

• Resultados Mixtos: Necesidad de acciones para reducir la variabilidad y centrar el proceso.

Ejemplo 3: Variables con Valores No Convenientes

Contexto:

• Proceso: Producción de envases plásticos.
• Variable: Espesor de la pared.
• LIE: 0.95 mm.
• LSE: 1.05 mm.
• Target: 1.00 mm.

Datos Recolectados:

• n: 30.
• Xˉ: 1.08 mm.
• σ: 0.02 mm.

Cálculos:

1. Tz:

Interpretación: Tz >> 0.5; corrimiento extremo.

1. Cr:

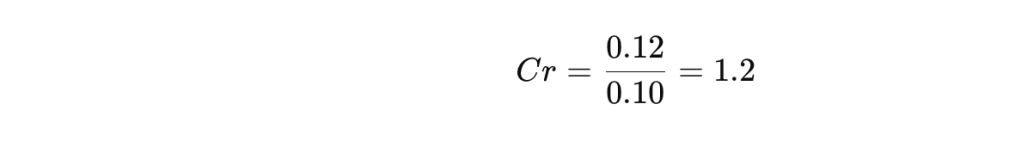
Interpretación: Cr > 0.75; variabilidad alta.

1. Cp:

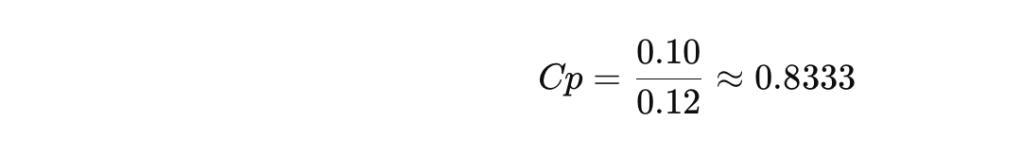
Interpretación: Cp < 1; proceso no es capaz.

1. Cpk:

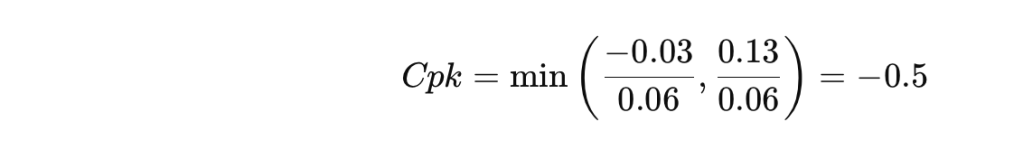
Interpretación: Cpk negativo; proceso fuera de especificación.

Interpretación Gráfica:

• Tz:
  • La curva de distribución está significativamente desplazada hacia la derecha, lejos del valor objetivo.
• Cr:
  • La distribución es relativamente estrecha, pero debido al corrimiento, la mayor parte de la curva está fuera de los límites de especificación.

Conclusión:

• Resultados No Convenientes: Acciones inmediatas son necesarias para corregir el corrimiento y reducir la variabilidad.

Recomendaciones

Para Procesos Satisfactorios

• Mantener Monitoreo Continuo: Asegurar la estabilidad del proceso.
• Mejora Continua: Buscar oportunidades para optimizar el proceso.

Para Procesos con Variables Mixtas

• Análisis de Causas: Identificar causas de corrimiento y variabilidad.
• Plan de Acción: Implementar medidas para centrar el proceso y reducir la variabilidad.
• Capacitación: Formación del personal en prácticas de control de calidad.

Para Procesos con Valores No Convenientes

• Acciones Inmediatas: Detener la producción si es necesario.
• Revisión Completa: Evaluar maquinaria, materiales y métodos.
• Asistencia Experta: Consultar a especialistas en procesos.

Razones Detrás de los Criterios de Éxito

Cp ≥ 1.33 y Cpk ≥ 1.33

• Margen de Seguridad Adecuado:
  • Un Cp y Cpk altos proporcionan un margen suficiente para variaciones menores sin comprometer la calidad.
• Reducción de Defectos:
  • Disminuye significativamente la probabilidad de producir productos fuera de especificación.

Tz < 0.5

• Control del Corrimiento:
  • Asegura que el proceso está centrado en el objetivo, reduciendo el impacto de variaciones sistemáticas.
• Calidad Consistente:
  • Mantiene la uniformidad en la producción, satisfaciendo las expectativas del cliente.

Cr < 0.75

• Variabilidad Controlada:
  • Un Cr bajo indica que la variabilidad está bien dentro de los límites aceptables.
• Zona de Seguridad:
  • Proporciona un margen del 25% del rango de especificación para absorber variaciones inesperadas.

Importancia de las Interpretaciones Geométricas

Las interpretaciones geométricas de Tz y Cr facilitan la comprensión visual de cómo la variabilidad y el corrimiento afectan al proceso.

Tz (Corrimiento)

• Visualización del Desplazamiento:
  • Muestra gráficamente cómo el promedio del proceso se desvía del valor objetivo.
• Identificación de Tendencias:
  • Ayuda a detectar patrones de corrimiento que pueden requerir ajustes.

Cr (Variabilidad)

• Comparación con el Rango de Especificación:
  • Permite visualizar si la distribución del proceso está dentro de los límites de especificación con margen suficiente.
• Evaluación del Margen de Seguridad:
  • Ayuda a comprender cuánto margen hay para tolerar variaciones adicionales.

Beneficios:

• Comunicación Efectiva:
  • Facilita la explicación de resultados a otros miembros del equipo y a la dirección.
• Decisiones Informadas:
  • Proporciona una base sólida para implementar mejoras y justificar inversiones.

Conclusión

La implementación efectiva de una estrategia de control de proceso utilizando el promedio, la desviación estándar, Tz, Cr, Cp y Cpk es fundamental para garantizar la calidad y eficiencia en la producción. Estas herramientas permiten:

• Diagnosticar el Estado del Proceso:
  • Identificar si el proceso es capaz y está centrado adecuadamente.
• Implementar Mejoras Dirigidas:
  • Enfocar esfuerzos en reducir la variabilidad o corregir el corrimiento según sea necesario.
• Monitorear el Progreso:
  • Evaluar el impacto de las acciones correctivas y ajustar estrategias.

---

Implementación Exitosa:

• Diagnóstico Preciso: Identificar problemas específicos del proceso.
• Acciones Correctivas Efectivas: Basadas en datos y análisis estadísticos.
• Monitoreo y Mejora Continua: Para mantener el control y optimizar el proceso.

• Comprensión Profunda:
  • Más allá de calcular índices, es crucial entender lo que significan y cómo afectan al proceso.
• Colaboración Multidisciplinaria:
  • Trabajar en conjunto con producción, mantenimiento y otros departamentos para implementar mejoras efectivas.
• Compromiso con la Mejora Continua:
  • Adoptar una cultura de excelencia que busque constantemente optimizar procesos y satisfacer al cliente.